Dynamics and Information of
"simple" neural networks

One of the fundamental hypothesis behind modern neuroscience is that emergent patterns observed in neural systems somehow converge to produce both low level behaviour (motor patterns, sensing, learning, etc) and high level cognitive processes (sentiments, conscience itself, etc); the core ingredients to maintain life. One of the key mechanisms underneath the generation of such complex patterns is in the coordinated dynamics of neural circuits and networks. We are, however, just scrapping the surface in terms of understanding of how patterns encode information, or how this information is furhter combined to sustain life itself. In this sense, we may ask...

Central Pattern Generators are among the favourite systems used to answer such questions. They are usually small circuits, capable of generating rhythms in an almost self-sufficient fashion. Even when detached from the nervous system, if appropriately maintained (chemically and physically), they can sustain their rhythm indefinitely. This robustness make them perfect circuits to maintain vital patterns, such ass breathing, cardiac cycles, chewing, walking, etc.

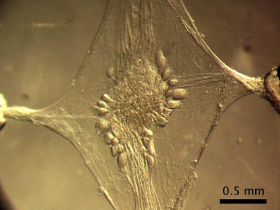
Figure 1: A photo of a crab's CPG. Each ball is the soma of a neuron.

One example of such network is the Stomatogastric Nervous System of crustaceans (Figure 1), studied for over 30 years. Prof. Reynaldo Pinto, our group leader, brought this research in the earlier 2000's to Brazil, in our lab. Particularly, he focused on a specific ganglion composed by few tens of neurons, known as Stomatogastric Ganglion (STG). Its main function is to generate peristaltic movements in the crustaceans intestine that push food inward to be digested. Especially because this is a rather small circuit, it's well studied and its neurons are well categorized in terms of their intrinsic dynamics and function. It's connectivity is also well accepted throughout the scientific community, which makes the STG a perfect benchmark to understand rhythms generation and information processing/transmission.

As physicists, our main interest is to understand these aspects using Information Theory, Dynamical Systems and Signal Processing. We show next some of the conclusions we got by using these mathematicals tools:

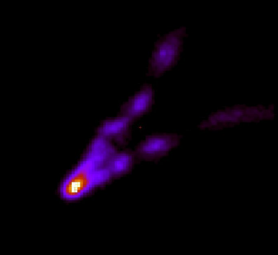
Figure 2: First return map (see text) of a neuron in the Stomatogastric Ganglion (STG). The patterns seen in these maps are almost unique signatures of each neuron in the STG, summarizing inner properties of its dynamics.

Despite the old belief that nerons are just "conductors" to transmit the information and the processing actually occurs on the set of synapses on the soma, nowadays there are plenty evidence that each neuron has its own dynamics that can be tuned by protein expression or chemical concentrations. On the stomatogastric ganglion we have shown that each neuron can be individually described by the its geometry of his "First Return Map". To construct this map, we take each spike we recorded and plot (i) in the x-axis the time interval between this spike and its predecessor - i.e., the previous spike; (ii) in the y-axis we insert the time interval between this same spike and the next one. We show an example in Figure 2. Finally, the color represents the quantity of points on that region: the mor clear, the higher the number of points in a particular region. What makes Frist Return Maps so interesting, especially in STGs, is that they carry a lot of information regarding the inner properties of the underlying dynamics of the neuron being analyzed. In fact, the patterns seen in these maps work almost as unique signatures, distinguishing neurons with markedly different behaviors and dynamics. These "shapes" also depend on the connectivity of the network.

By connecting neurons to computer models using electrodes that can inject a current dependent of the electric activity (Dynamic Clamp protocol), we also measured the information quantity (in bits) that is transmitted in a single synapse between cells of the stomatogastric ganglion, reflecting how much "degrees of freedom" the circuit can tune, how much behaviours it can assume.