Large Networks Simulations
This text is still under development.After you have a basic model that should describe a phenomenon, you can simulate your model for basically two reasons: (i) validate the model and learn its limits of application; (ii) make new hypothesis and suggest new experiments. Several scientists believe that being able to describe an effect in mathematical terms and reproduce it in silico is the ultimate endgame in understanding the true nature behind the effect.
In our lab, We are especially interested in complex phenomena that can arise from large networks. In Statistical Physics, this is a widely spread notion: it's quite frequent that effects arising from simple, coupled units seem more complex than the sum of their effects separately.
Critical networks and psychophysics
One of our main interests rely on how complex behavior emerge from networks of simple neurons. Several network properties are believed to be enhanced whenever you tune your network to a very specific, (dis)organized state. This state oftenly lies in the border between two very distinct regions in terms of how the network behaves. Also frequently, the biological systems being studied tend to remain in these systems. Although the reason is not fully understood, it seems a very practical solution nature has found to optimize the operational properties of its systems. With this in mind, and importing notions from Out-of-Equilibrium Statical Physics, people call it a Critical State.
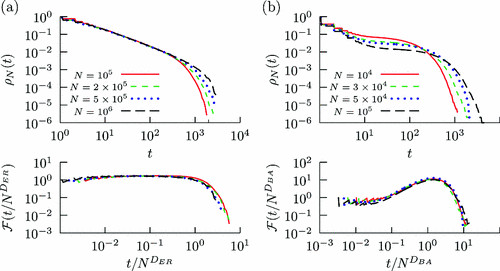
Let's focus our discussion: the dynamic range of a neural network measures the extent to which this network can understand the stimuli. In terms of audition: what's the range in frequency in which your years can distinguish between one note and another note? The size of this range (usually measured in decibels) is its dynamic range. For vision, you can think of the range of luminosity in which your eyes are able to distinguish how bright the light is.
The interesting thing is that models and experiments suggest that the dynamic range of a neural network is optimized in a critical state.
Below you'll find videos of simulations of a network in the three possible states: subcritical, critical and supercritical. The yellow dot represents the source of excitation: we are manually inducing spikes there with a fixed frequency. These simulations were designed using a square lattice, creating a natural spatial notion of neighbourhood. Notice how in the supercritical case, the activity seems to sometimes live undefinitely.
Dynamical (and complex) Systems
Critical systems are not the only source of interesting phenomena: the more realistic a models demand a considerable increase in the model complexity. For example, some conductance models may have 16 dimensions per neuron, i.e., there are 16 equations per neuron to be solved simultaneously. Don't forget they are all coupled! The advantage of having more realiastic dynamics is that you have a closer link between your model and the physiological parameters in the laboratory. However, there's a price to pay: the networks are usually smaller and you start having huge numerical challenges.
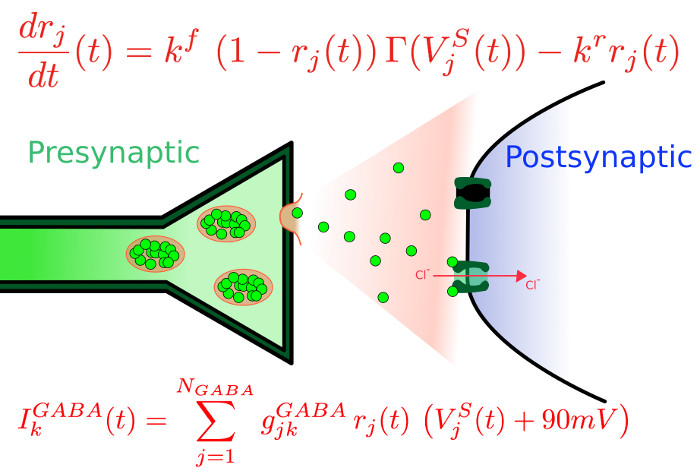
In this kind of model, synapses may play a very important role: the timing, mechanisms, chemicals, stages, etc. There is an ever growing repertoire of models that try to capture the most essential features to describe certain synapses. For instance, you can see in the above figure one way to implement a GABAergic synapse, in which Cl enters the cell and (usually) ends up in a hyperpolarization of the cell's membrane potential.
